28 Mar 2020
In this post, we’ll focus on a multi-part problem in chapter 1 of “Fundamentals
of Astrodynamics” by Bate, Mueller, and White, that introduces some basics of
orbit determination, namely eccentricity.
Exercise 1.8 Identify each of the following trajectories as either circular,
elliptical, hyperbolic, or parabolic:
a.
b.
c.
d.
e.
Solution:
Our goal to determine the type of orbit for all of the following will be to find
an expression of eccentricity, , based on our knowns. However, in some
cases it is unnecessary to solve for because often as an intermediate
step, it is necessary to find the specific mechanical energy, ,
which can at the very least inform of us as to whether the orbit is elliptical
(circular being a special case) ( < 0), parabolic
( = 0), or hyperbolic ( > 0). Prove this to
yourself be examining equations 1.4-2 and 1.6-4 from the book.
a.
Given a scalar position and velocity, and , respectively, we seek to
equate these to eccentricity. However, we cannot solve for only knowing
these two parameters. But luckily for us, these problems only require declaring
what type of orbit it is. As prefaced above, we can do that by solving for
specific mechanical energy, :
where is velocity, is position, and is the gravitational
parameter (for our purposes equal to unity due to working in canonical units).
Solving this yields a positive result:
The orbit is therefore hyperbolic. Let’s take this a step further and attempt
to solve for using equation 1.6-4 from the book to prove to ourselves this
is the case:
where is specific angular momentum. But what is ? We can’t solve
for an exact value for without knowing the flight path angle, ,
because and are scalars. But that doesn’t matter. We don’t care
what is as long as it’s not zero, which would only be the case for a
degenerate conic (essentially a point in space or straight line), because
is squared in the above equation. The leap in insight here is to see that
because one is being added to a positive number greater than zero under the
square-root, must be greater than one and therefore the orbit is a
hyperbola.
b.
We can solve for using the polar equation of a conic section knowing the
semi-latus rectum, , and that the periapsis distance, , occurs when
the true anomaly, , is zero as follows:
The resultant eccentricity being unity means the orbit is a parabola.
c.
Given and , we can use equation 1.6-4 from the text with a
simple substitution for the specific angular momentum, , and solve directly
for :
The resultant eccentricity being zero means the orbit is a circle.
d.
Only being given vectors for position, , and velocity, ,
we must find both and before we can solve for . The
specific angular momentum can easily be solved for using Sarrus’scheme
to find the cross-product:
The specific mechanical energy is a function of the scalars velocity and
position:
We can now solve for the eccentricity using equation 1.6-4 from the text:
The resultant eccentricity being less than one means the orbit is an ellipse.
e.
This final problem can be solved in the exact same way as the previous. For
brevity, I’ll skip any explanation and just show steps:
The resultant eccentricity being greater than one means the orbit is a
hyperbola.
02 Feb 2020
Moving on to the next problem in chapter 1 of “Fundamentals of
Astrodynamics” by Bate, Mueller, and White, we arrive at a simple proof.
Exercise 1.7 Prove that .
Solution:
By inspection of the figure in my previous post:
In simple language, apoapsis (i.e. maximum radial distance) happens 180
o, or radians from periapsis (i.e. minimum radial distance).
To show that , we’ll revisit equation 1.5-4 from the
book, a form of the trajectory equation called the polar equation of a conic
section:
where , is the radial distance from the focus as a function of the true
anomaly, , the semi-latus rectum, , and the eccentricity, . We
can substitute equation 1.5-6 for the semi-latus rectum and complete the proof:
19 Jan 2020
Continuing with “Fundamentals of Astrodynamics” by Bate, Mueller, and White,
but skipping around a little, it’s time for an easy one!
Exercise 1.6 Find an equation for the velocity of a satellite as a function
of total specific mechanical energy and distance from the center of the earth.
Solution:
Skipping the derivation for now (I’ll save that for another post) the equation
for specific mechanical energy, , is:
where is the velocity, is the gravitational parameter,
1.40765x1016 ft3s-2 for Earth, and is the
radial distance from the center of the earth to the satellite. Simply
rearranging for yields the desired equation:
07 Sep 2019
Again, we’re back in “Fundamentals of Astrodynamics” by Bate, Mueller, and White,
continuing with the first problem set.
Exercise 1.3 An Earth satellite is observed to have a height of perigee of
100 NM and a height of apogee of 600 NM. Find the period of the orbit.
Solution:
Unlike other questions in the book, this one does not come with an answer to
check your work against. Thus, it is important to ask yourself: does my answer
make sense? When I first solved this problem, I took 100 NM and 600 NM to be
the radius of perigee and apogee, respectively, not giving much thought to how
this would be an extremely small orbit “inside” the Earth. The answer of course
instantly made me realize my error and I then recomputed assuming the height to
be that of the satellite above the Earth’s mean equatorial radius of 3443.923 NM
as given in Appendix A. As you’ll see below, the solution given this assumption
is much more realistic, especially knowing the period of common low Earth orbit
objects such as the International Space Station.
To begin, the equation for the period, , of an elliptical orbit is:
where is the semi-major axis and is the gravitational parameter,
1.40765x1016 ft3s-2 for Earth. Recall that
can simply be calculated as:
where is the radius of apogee and is the radius of perigee.
These two radii can be found by adding the Earth’s mean equatorial radius,
, and the height of the satellite at the two respective positions:
where is the height of apogee and is the height of
perigee. Substituting these into our equation for yields:
Plugging in our knowns into our equation for the orbital period yields the
solution:
24 Aug 2019
Continuing with the first problem set in “Fundamentals of Astrodynamics” by
Bate, Mueller, and White, we arrive at what seems like simple problem. Given
the velocity and position of a satellite, find its eccentricity. However, as
simple as it seems, you’ll see it takes quite a bit of derivation to arrive at
the answer.
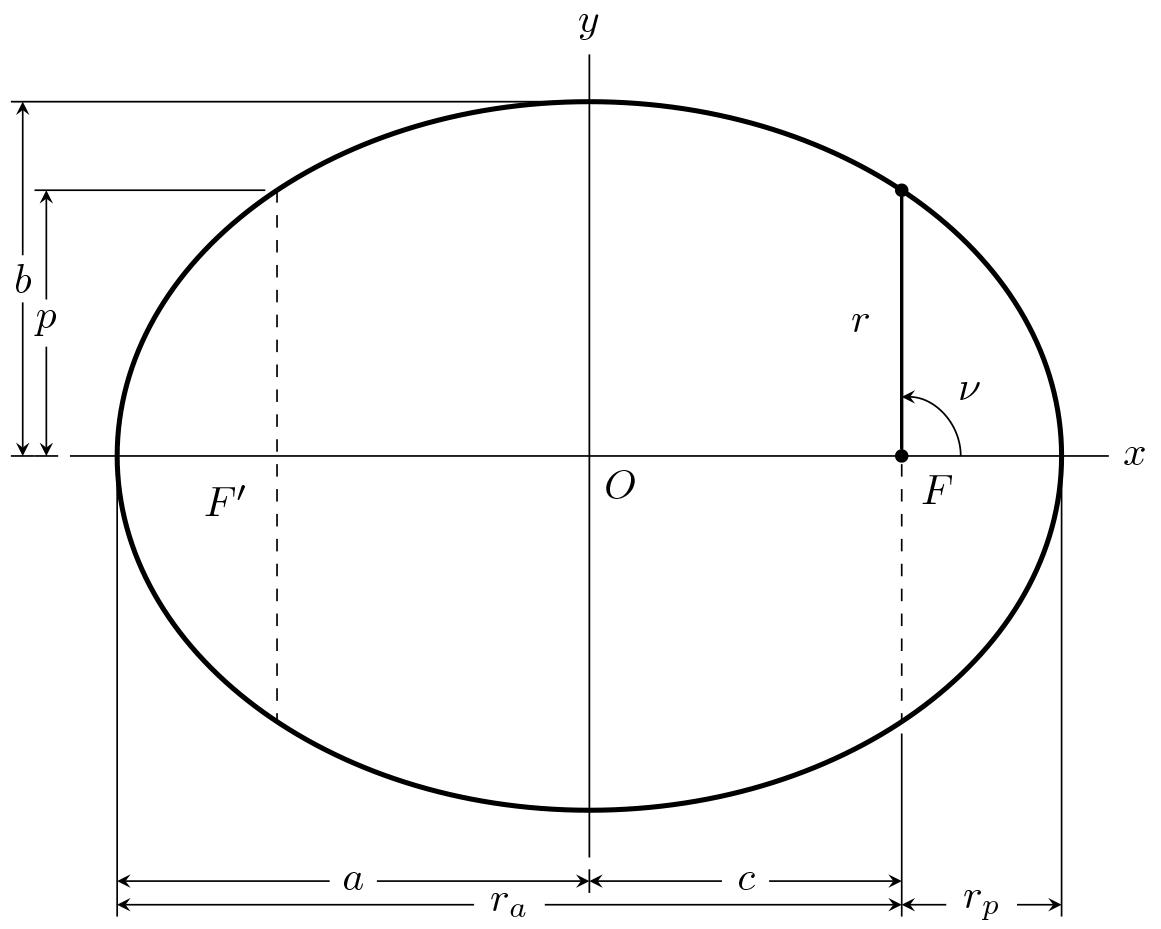
Exercise 1.2 For a certain satellite the observed velocity and
radius at is observed to be 45,000 ft/s and 4000
NM, respectively. Find the eccentricity of the orbit.
Solution:
To begin, by inspection of Figure 1.5-1 in the book or the figure above,
when . We can also show this mathematically
using the polar equation of a conic section:
where is the radius, is the semi-latus rectum, and is
the eccentricity.
Using equation 1.5 between the semi-major axis, , and the semi-latus
rectum, , we can solve for eccentricity:
Now we need to find, . This can be done using the relationship between
and the specific mechanical energy, :
where is the gravitational parameter, 1.40765x1016
ft3s-2 for Earth.
Substituting this into our equation for yields:
Recall that the equation for specific mechanical energy is:
Substituting this into our equation for above, with a little rearranging,
gives us eccentricity in terms of our knowns:
Now the calculation for eccentricity can be done being mindful of units (1 NM =
6076.12 ft):
which means the orbit is hyperbolic.

